One-Dimensional Motion/Free fall


Introduction

Now comes the fun (depends on your definition) part of physics! All these equations and values that we just learned are meaningless if we cannot apply them! Thus, we begin with a the simple example of 1-dimensional motion. Since we are doing 1-dimensional motion, you can, in fact, treat everything as if they were scalars. If you think about it, a one-dimensional vector IS a scalar, since its just one number to represent it! Now, this chapter and the next chapter will be understanding some important concepts, but still mostly problem solving. As such, I've made a very simple interactive demo with matter.js for you to play around with that illustrates the concept of free fall.

Free Fall Demo



Input how "bouncy" you want the blocks to be, from 1 to 10.
Values over 10 may result in some odd and unrealistic behaviors.
Notice how the objects that are falling hit the ground at the same time, even though their masses and shapes are different? They may bounce around differently after hitting the ground, but the time they first hit the ground is the same for all of the objects! This is generally true: the gravitational acceleration of an object is independent of its mass. The reason we see some things fall slower than others is because of air resistance. Now, with that little observation out of the way, we may begin.

Since we are dealing more with physics concepts, there will be some important things to clarify and brush up on, and guess what: ZERO problems to solve in this chapter! It's just 100% concepts. One generally important thing that we kindly avoided mentioning was the fact that, air resistance and friction, in the real world, indeed does exist. However, for the sake of simplicity in our calculations, most of these entry level kinematics will ignore air resistance and friction, and assume all the objects that we deal with are ideal in the sense that they don't generate a lot of air resistance nor friction.

The Equations

We generally will be less focused on doing calculations, but here are the equations that we will be needing anyways (the Basic Algebra lesson would be very very helpful right now!): $$\underline{\textrm{\#1:}~~v_f=v_0+at}$$ $$\underline{\textrm{\#2:}~~x=v_0t+\frac 1 2 at^2}$$ $$\underline{\textrm{\#3:}~~x=v_ft-\frac 1 2 at^2}$$ I know I've omitted the "$\Delta$" symbol for displacement ($x$) and time ($t$), but just know that it means "change in". It just becomes a lot simpler to write things that way.

Furthermore, in the previous chapter, we used $v_i$ to denote initial velocity, but we used $v_0$ here. Just make a mental note that both refer to initial velocity, it just depends on the naming convention you prefer. If you were reading the previous lesson, you know exactly how we derived these two equations. If not, there's no harm in going back for a refresher! Now there are some other cool equations that we didn't show you how to derive waiting for you on the next page! Before we get into solving problems (fun!), one generally important thing that we kindly avoided mentioning was the fact that, air resistance and friction, in the real world, indeed does exist. However, for the sake of simplicity in our calculations, most of these entry level kinematics will ignore air resistance and friction, and assume all the objects that we deal with are ideal in the sense that they don't generate a lot of air resistance nor friction.

The Equations

If you have already forgotten (which I hope you haven't), here are the equations we derived from the previous chapter: $$\underline{\textrm{\#1:}~~v_f=v_0+at}$$ $$\underline{\textrm{\#2:}~~x=v_0t+\frac 1 2 at^2}$$ I know I've omitted the "$\Delta$" symbol for displacement ($x$) and time ($t$), but just know that it means "change in". It just becomes a lot simpler to write things that way.

Furthermore, in the previous chapter, we used $v_i$ to denote initial velocity, but we used $v_0$ here. Just make a mental note that both refer to initial velocity, it just depends on the naming convention you prefer. If you were reading the previous lesson, you know exactly how we derived these two equations. If not, there's no harm in going back for a refresher! Now there are some other cool equations (and yes that you probably should memorize) that we didn't show you how to derive. Here they are now: $$\bar{v} = \frac{v_f+v_0}{2}$$ The average velocity is calculated from taking the average of starting and end velocities. But we know that $x=\bar{v}t$, so if we multiply both sides by $t$, we get: $$\underline{\textrm{\#3:}~~x= \frac{v_f+v_0}{2}\cdot t}$$ Now lets focus on deriving arguably one of the more common equations that you will come across. Now we just derived an equation that looks pretty handy. So let's start from there. Now, one of the most basic equations is $v_f=v_0+at$. If we solve for $t$, we get: $$t=\frac{v_f-v_0}{a}$$ So now we can plug this into the equation we just derived: $$x= \frac{v_f+v_0}{2}\cdot \frac{v_f-v_0}{a} = \frac{(v_f+v_0)(v_f-v_0)}{2a}=\frac{v_f^2-v_0^2}{2a}$$ Deriving this shows us that we do not necessarily need to know the time period in order to calculate other quantities! Rearranging the equation a little bit will give us the final result: $$\underline{\textrm{\#4:}~~v_f^2=v_0^2+2ax}$$ Now, all these four equations that we just listed are super useful. You can use them to solve various kinematics problems! However, there is one small important detail that I have left out. All these equations are ONLY valid when acceleration is constant. Without constant acceleration, all these wouldn't work, and we would have to resort to calculus tools to help us solve those problems.

There's a final equation that's useful sometimes. It's very similar to the second equation, but uses final velocity rather than initial. I'll lay it out for you here. You might (correctly) assume that this is only useful when you're given final velocity rather than initial. $$\underline{\textrm{\#5:}~~x= v_f t - \dfrac12 at^2}$$ Another really cool thing about all those kinematics equations is that we have five quantities: $x$, $v_f$, $v_0$, $a$, and $t$. Each of the five kinematics equations that we have laid out (scroll up if you need to see them again, they're numbered!) has exactly four quantities in them, which means each equation is not using one of the five quanitites! Can you spot in each equation which quantity is missing? Realizing the dependency on one another that each of these five quantities exhibits is crucial and knowing this can really level up your game and make you better at deciding what equation to use to solve a problem. And because we are doing algebra-based physics, we want you to solve problems! So let's get into it.

Here are the equations (like we promised): $$\bar{v} = \frac{v_f+v_0}{2}$$ The average velocity is calculated from taking the average of starting and end velocities. But we know that $x=\bar{v}t$, so if we multiply both sides by $t$, we get: $$\underline{\textrm{\#4:}~~x= \frac{v_f+v_0}{2}\cdot t}$$ Which is another super useful equation. Obviously, if you don't intend to do calculations with your physics knowledge and you just want to grasp the concepts, you can skip the next section.

Now lets focus on deriving arguably one of the more common equations that you will come across. Now we just derived an equation that looks pretty handy. So let's start from there. Now, one of the most basic equations is $v_f=v_0+at$. If we solve for $t$, we get: $$t=\frac{v_f-v_0}{a}$$ So now we can plug this into the equation we just derived: $$x= \frac{v_f+v_0}{2}\cdot \frac{v_f-v_0}{a} = \frac{(v_f+v_0)(v_f-v_0)}{2a}=\frac{v_f^2-v_0^2}{2a}$$ Wow! That's amazing. This shows us that we don't even need to know the change in time to calculate the displacement! Rearranging the equation a little bit will give us the final result: $$\underline{\textrm{\#5:}~~v_f^2=v_0^2+2ax}$$ Now, all these five equations that we just mentioned are super useful. You can use them to solve various kinematics problems! However, there is one small important detail that I have left out. All these equations are ONLY valid when acceleration is constant. Yup, without constant acceleration, all these wouldn't work, and we would have to resort to calculus tools to help us solve those problems (and if you're here like me, you probably don't know calculus).

The first problem will test you how well you can apply these equations into basic mechanics:
A car accelerates from rest in the positive x-direction with a magnitude of $1.5~\textrm m / \textrm s ^2$ for $5\textrm s$. Find its...
a) Final velocity
b) Displacement

When starting to solve this problem, the first step you always take is to list what values are known and what you are solving for. You should have three known values, since we mentioned that each equation contains four quantities, and you only need one equation to solve for one unknown. But you might be saying, the problem only gives us two known values, the acceleration, and the time interval! Upon closer inspection, however, you may have noticed the words from rest were italicized. You might be wondering, what in the world does this tell us?? Well, "rest" is when you are not moving. And if you are not moving, your velocity must be zero. So if you start from rest, your initial velocity must be zero. The key thing about these sort of problems is to read the question and see if you can pull out any other information that is not explicitly stated. So now we have our knowns: $v_0=0 ~\textrm m / \textrm s$, $a=1.5 ~\textrm m \ \textrm s ^2$, and $t=5\textrm s$, let's solve for part a, the final velocity. Now, what quantity is missing? Displacement. So we find that equation $\#1$ (scroll up) gives us the desired answer. Plugging in the values will give us: $$v_f=(0)+(1.5)(5)=\bbox[3px, border: 0.5px solid white]{+7.5 ~\textrm m/\textrm s}$$ We have omitted the units here, but if you feel the need to put in the units, there's no harm in doing so. It can help you get some insight as to whether you did the problem correctly. Furthermore, you may have noticed the plus symbol in front of our answer. This is because everything has happened in the positive direction, as the problem stated. If this was in the negative direction, you should put the negative signs where necessary. Do note that it is always important to solve the equation for the unknown value, instead of just doing what is called "plug-and-chug". So if the problem instead were asking for initial velocity, you would solve the equation (isolate the variable on one side) for $v_0$. This has a super important meaning I'll discuss later on. Next, let's work on part b.

For part b, before we start solving, you may realize that we actually have four known values now, so we can technically use any equation we want to solve for displacement. However, it is generally advised to only stick with the values that you are given. One major reason is that when you begin to deal with more complex problems, there will be times when you must round off your answer. Rounding off is normal, but when you use that rounded number to calculate other unknown values, it creates a rounding error and will make your answer more inaccurate. Thus, we will only use the given values, $v_0,a,t$ to solve this problem. If you haven't already noticed, we must use equation $\#2$ (again, scroll up) to solve this problem. Since the equation is already in the form of $x=...$, we can directly plug in the values: $$x=(0)(5)+\frac 1 2 (1.5)(5)^2=\bbox[3px, border: 0.5px solid white]{+18.75 ~\textrm m}$$ This is our answer for part b.

Here is the video explanation for this problem, if you prefer that:

Another really cool thing about all those kinematics equations is that we have five quantities: $x$, $v_f$, $v_0$, $a$, and $t$. Each of the five kinematics equations that we have laid out (scroll up if you need to see them again, they're numbered!) has exactly four quantities in them, which means each equation is not using one of the five quanitites! Can you spot in each equation which quantity is missing? Realizing the dependency on one another that each of these five quantities exhibits is crucial and knowing this can really level up your game and make you better at deciding what equation to use to solve a problem.
Now as I said, there is ZERO problem solving in this chapter, so we will introduce another interesting concept!

Free Fall

One-dimensional motion, all in all, seems pretty boring. However, there is a case where you can virtually immediately apply it to your everyday lives. Well, what is that? It's free fall!
Figure 1: A guy pushing his friend off a cliff.
(Note: I do not officially condone pushing people off of cliff faces, it is very dangerous. But what you do is ultimately up to you.)
For problem two, we are going to make things a little more interesting. See if you can do it on your own, before looking at our solution. Here's the problem:
A ball is observed to move for $15~\textrm m$ in the negative x-direction for $3\textrm s$. The magnitude of final velocity of the ball is recorded to be $8~\textrm m / \textrm s$. What was its acceleration?

This problem can seem a little daunting at first, but let's list our known values: $x=-15~\textrm m$, $v_f=-8 ~\textrm m / \textrm s$, $t=3\textrm s$. If you don't understand why there's a negative sign, remember that we said the ball in the negative x-direction? Although we said the magnitude of the final velocity, we didn't state its direction. However, from other information that we give you, you can 100% assume that the direction of the final velocity also must be in the same direction as the displacement. So if the displacement is negative, the direction of the final velocity must also be in the same direction (can you see why?)!
If you're looking at the equations we gave you, you might realize that there's no equation that is missing $v_0$! So we will have to derive it ourselves. Remember our equations $v_f=v_0+at$ and $x=\frac{v_f+v_0}{2}t$? So what we lack is $v_0$, so we need to solve for $v_0$ in our first equation. Solving gives us $$v_0=v_f-at$$ And plugging this into our other equation gives us: $$x=\frac{v_f+v_f-at}{2}t=(v_f - \frac 1 2 at)t=v_ft-\frac 1 2 at^2$$ You can memorize this equation if you like, however, it doesn't pop up nearly as much from what I've seen, so it's entirely up to you. Of course, you could do a quick derivation like we just did. Now we need to rearrange the equation for acceleration, since it is what it asked for. $$x-v_ft=-\frac 1 2 at^2$$$$at^2=2(v_ft-x)$$$$a=\frac{2(v_ft-x)}{t^2}$$ Pluggin the values in gives us: $$a=\frac{2((-8\cdot 3)-(-15))}{3^2}=\bbox[3px, border: 0.5px solid white]{-2 ~\textrm m / \textrm s ^2}$$ This should give you a good idea of how to approach problems. You also noticed very well how we kept the equations in symbols and plugged everything in at last. This may seem very foolish and unappealing to you at first, but when you get to the difficult problems, it will become more relevant. If you simply put in the numbers right away, you would have the issue of dealing with numbers, instead of being able to simply do the algebra first and getting a single equation where you can just plug in the values in one go. This also has a more significant meaning that will be explained later on.

Free fall is not something new, it's just a special case of kinematics where our constant acceleration is not just something random like $7$, $29$, or $2.72$ $\textrm m/\textrm s ^2$. It is a case where the magnitude of $a$ is specifically equal to $9.81$, or sometimes approximated as $9.8$ or $10~\textrm m/\textrm s ^2$ (on Earth, at least. You'll learn more in the unit about Circular Motion and Gravitation!). This value is called the acceleration due to gravity, represented with the letter $g$ (hang on! If this is confusing, think of $g$ as a constant, a value that doesn't change unless you're on a different planet! We will introduce a different definition much later on, but just know that is a constant* on earth!). Basically, all objects will fall at this rate when released into free fall (neglecting air resistance).

Now if you are clever, you noticed how we said "all objects". But wait! Doesn't the mass affect how fast it falls? Well, your intuition is once again, incorrect! You may have also noticed mass never existed in our kinematics equations in the first place! In short, the derivation as to why this is true is beyond the scope of our current knowledge by just a few lessons. So we will revisit this problem once again. However, in the case where there IS air resistance, your intuition is *somewhat* correct! You might have also heard of terminal velocity, and that's what air resistance plays a role in. But, we are getting ahead of ourselves! So let's all assume that friction and air resistance are negligible, and continue on. Now, all of our kinematics equations STILL work in the the realm of free-fall, because the acceleration is constant!

Free Fall

One-dimensional motion, all in all, seems pretty boring. Despite this, it is a necessary skill that you learn how to work with when we hit 2-dimensional motion. Yet, there is a case where you can virtually immediately apply it to your everyday lives. Well, what is that? It's free fall!
Figure 1: A guy pushing his friend off a cliff.
(Note: I do not officially condone pushing people off of cliff faces, it is very dangerous. But what you do is ultimately up to you.)
Free fall is not something new, it's just a special case of kinematics where our constant acceleration is not just something random like in our previous questions, it is a fixed value. It is a case where the magnitude of $a$ is equal to approximately to $9.81$, or sometimes approximated as $9.8$ or $10~\textrm m/\textrm s ^2$ (on the surface of Earth, at least. You'll learn more in the unit about Circular Motion and Gravitation! For all problems that involve $g$, assume we are on Earth unless otherwise stated). This value is called the acceleration due to gravity, represented with the letter $g$. Basically, all objects will fall at this rate when released into free fall (neglecting air resistance). Another thing that is different is that instead of $\Delta x$, or just $x$, is expressed as $\Delta y$ or just $y$, since now we are in the vertical direction.

Now if you are clever, you noticed how we said "all objects". But wait! Doesn't the mass affect how fast it falls? Well, your intuition is once again, incorrect! You may have also noticed mass never existed in our kinematics equations in the first place! In short, the derivation as to why this is true is beyond the scope of our current knowledge by just a few lessons. So we will revisit this problem once again. So let's all assume that friction and air resistance are negligible, and continue on. Now, all of our kinematics equations STILL work in the the realm of free-fall, because not only is our acceleration constant, it's fixed!
There are some quirky things about free fall. First of all, what we define as the positive and negative direction can be a little tricky. If we define the positive direction as upwards, then our $\Delta y$ is equal to $-h$, the opposite of the total height the object fell, and the sign of $g$ would be negative. If the positive direction is defined to be downwards, then then our $\Delta y$ is equal to $h$, the opposite of the total height the object fell, and the sign of $g$ would be positive instead. You can think of $\Delta y$ (or $y$) as the displacement in the vertical direction, while height ($h$) is just a fancy way to say distance but in the vertical direction. Since it is standard, we will define the positive direction as upwards.

The New (not really) Equations

Problem solving is very, very straightforward. The equations are tweaked a little bit since we defined our positive direction as upwards (for those involving $a$). You'll see how this affects our values when we solve problems: $$v_f=v_0-gt$$ $$y=v_0-\frac 1 2 gt^2$$ $$y=v_f+\frac 1 2 gt^2$$ $$v_f^2=v_0^2-2gy$$ The reason why we put a negative sign in front of our terms involving $g$ is because we treat $g$ as the absolute value of itself, so essentially it's just a positive scalar with a value of $9.81~\textrm m/\textrm s ^2$. However, there are two directions in one-dimensional motion, positive and negative, so we need a negative sign. Since our positive direction is upwards, all of our values should be pretty much negative since our objects are falling downwards. There are exceptions though! Now let's use these equations to solve some problems.

Free Fall Concepts

Since we introduced the concept of free fall, let's take a look at some important concepts regarding free fall. Have you ever noticed that when you toss something into the air, it slows down, and then comes back downwards? This is because our acceleration is downwards, always. One common pitfall that people make is that the acceleration must always point in the same direction as the motion of an object. They might say since the object is traveling upwards, its acceleration must point upwards. No! This is wrong! The acceleration due to gravity always points toward the center of earth, never towards outer space! If you've noticed before, the object is slowing down, and comes the other way, which means briefly, at some point in time, its instantaneous velocity must be zero. And it just so happens that it is at the peak of the object's motion!

Also, another really cool thing about if you do this is that, the time for the object to reach the top is half the total time it takes to come back down at you. And if its velocity at the peak is zero, then half the time is spent from your velocity going from $v_0$ to $0$. Now since the acceleration is constant, the velocity must undergo the same change in the second half of the time, so it goes from $0$ to $-v_0$. This proves that, when you throw something into the air (neglecting air resistance), and you catch it, it comes down at the exact same magnitude of velocity, but the direction is opposite! You can try testing your friends and family on this concept, if you throw a rock vertically down a cliff and throw one upwards at the same magnitude of velocity, which one will impact the ground with more velocity, or will they be the same? You know the answer—it's yes!
An object is dropped from rest and falls a distance of $15 ~\textrm m$. How much time did it take to fall down? Then, find the magnitude of the velocity it impacts the ground with.
Before you complain about the lack of information we provided to you, remember that this is a scenario of free fall, which means the magnitude of our acceleration is $9.81~\textrm m / \textrm s ^2$. "From rest" means that $v_0=0$, as previously mentioned before. There's our three values that we need! Now let's solve for $t$ and $v_f$. One important thing to note is that the object does have final velocity before it hits the ground, even though it comes to a rest after hitting the ground (if it doesn't bounce). So when we say final velocity in the realm of horizontal kinematics, just remember it's the velocity the object impacts the ground with. Solving for $t$: $$y = (0)t-\frac 1 2 gt^2$$ $$t=\sqrt{\frac{-2y}{g}}=\sqrt{\frac{-2(-15)}{9.81}}≈\bbox[3px, border: 0.5px solid white]{1.75\textrm s}$$ A quick analysis of the problem: Remember that since the positive direction is upwards, your displacement is $-h$ when you move downwards (dropping an object in our case). So in this case, $y=-15~\textrm m$. You might notice that there is a negative sign in our square root, but it becomes cancelled out due to the fact that our displacement is negative. Also, time doesn't have a positive or negative sign. It is always a positive scalar, so there is no need to indicate so. Now let's solve for the final velocity. Now you see here is where we run into a problem. If we tried using the calculated value for the time for the object to fall down in our calculation for the final velocity, there would be a slight deviation than if we used the given values. This is because our value of the time is rounded, and not exact! So let's use the equation without time. If you don't remember, it's $v_f^2=v_0^2-2gy$. Solving for $v_f$: $$v_f=\sqrt{(0)^2-2gy}=\sqrt{-2gy}=\sqrt{-2(9.81)(-15)}≈\bbox[3px, border: 0.5px solid white]{-17.1~\textrm m / \textrm s}$$ By the way, you may have noticed we plugged in the value of $0$ for $v_0$. You might be thinking, didn't you tell me not to plug in numbers yet? Well $0$ is an exception. Sometimes, when plugging it in, it can make your math easier. For example, we would have needed quadratics to solve for $t$, but by plugging in, we only needed to take a square root. So, now that we've gotten a taste of free fall, let's maybe perhaps move onto a more challenging question.


Try and solve this problem yourself before looking at the solution:
Maurice accidentally drops a statue that was originally sitting still out the 5th story window, $25~\textrm m$ above the ground. He yells to a passerby, "WATCH OUT!!" after it drops $3~\textrm m$. How long does the poor guy have to get out of the way?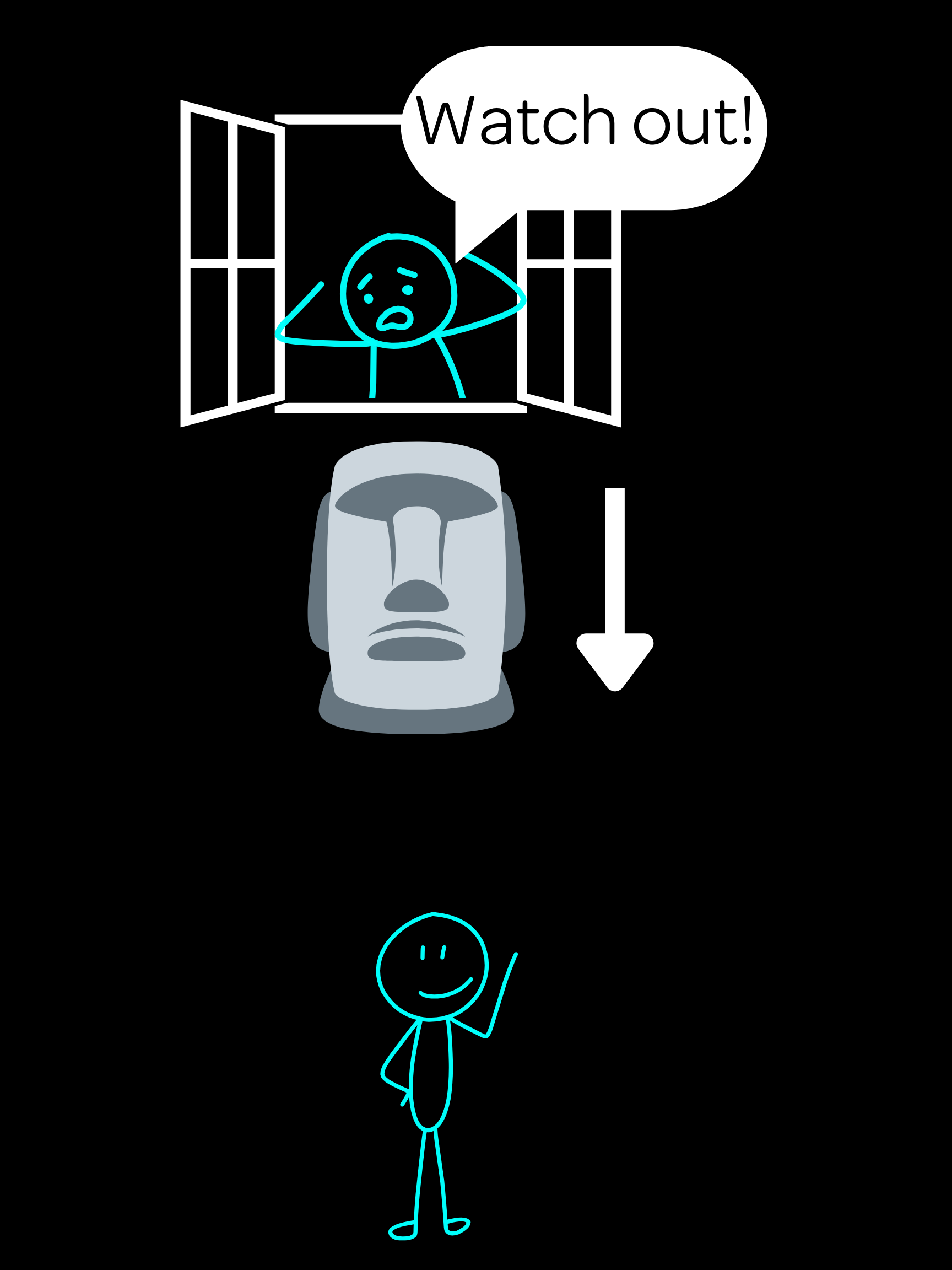
Figure 2: An innocent passerby that will soon be flattened (*Not drawn to scale).

At first, this problem seems quite daunting. There are quite a few approaches you can go about for solving this problem, like say maybe you realized that our final velocity after dropping $3~\textrm m$ is our initial velocity for the rest of our drop, but then you might have realized we need to do quadratics for that, which is definitely not ideal. But you might have realized that the total time, $t_{total}$, minus the time it falls the $3~\textrm m$, which we will call $t_1$, is the time it falls the rest of the way! And here's how we calculate it. Since $v_0=0$ when we calculate both times, as both cases start from the top, we can use $t=\sqrt{\frac{-2y}{g}}$ from the previous problem to help us out here. $$t_{total}=\sqrt{\frac{-2(-25)}{9.81}}$$ $$t_1=\sqrt{\frac{-2(-3)}{9.81}}$$ $$t=\sqrt{\frac{-2(-25)}{9.81}}-\sqrt{\frac{-2(-3)}{9.81}}≈\bbox[3px, border: 0.5px solid white]{1.48~\textrm s}$$ This is not a lot of time for the passerby to react at all! Considering the average human reaction time is 250 milliseconds, the time with that, and the fact the guy needs to process the situation, he will not likely come away unscathed.

This was a rather brief lesson, and I promise there are much more interesting concepts in the next lesson. It is much more applicable because you can experiment and see it in your everyday lives, manifested in the form of not 1-dimensional, but 2-dimensional motion, also known as: projectile motion!

Conclusion

Before we get into it, as always, I have something for you to chew on (no, not literally). If you didn't understand any bit of the equation part of the chapter, that's okay! Not everyone knows algebra 1 and that was an important part of creating this project in itself. Yet despite this, I still want you to go back to the underlined equations and try looking at it again to see if you notice anything. You probably didn't, right? So now I will tell you why what you looked it is what makes physics beautiful (and why all of science is beautiful). Some of you may have come into this course thinking that physics is just a bunch of nonsensical mathematical junk. And to a reasonable extent, some of that is most definitely true.

But here is what draws the distinction between us physicists and mathematicians. To your average mathematician, that is just an equation with a bunch of variables, and they see it as a mathematical tool, a placeholder, for something that they will use later to solve equations. But for physicists, the meaning of this goes way deeper. If you take a look at how we derived $x=v_0t+\frac 1 2 at^2$ in the previous chapter, you can see us doing a seemingly complex process just obtain such a simple thing. From a math perspective, it is a lot of hard work, but if you look at more in depth at how we went through it, how we touched upon many different physics concepts that we just learned, how we combined what we knew to find something that we didn't know, and how we ended up with such a beautiful result, you'll observe that this equation over here doesn't just contain the mathematical meaning it carries in solving problems.

Going back to our example, you'll see that $x$, our displacement, is dependent on three things: the initial velocity multiplied by the time interval, and add one-half the acceleration multiplied by the time interval squared. By realizing this dependency and interconnection between all these four quantities, you now know how the physics as to how all these quantities are related to each other and how they interact with each other. You are able to see that our equations, in physics, not only carry mathematical importance, but physical importance as well (physical referring to physics). Sometimes, physics is so seemingly complex, but it produces such elegant and simple results.
And sometimes, simple is beautiful.

Free Fall w/ Upward Motion

Before we continue on to 2-dimensional motion, there is an important concept that needs to be covered. What if, instead of dropping something, you threw it upwards? You would see the object rise but then slow down, then come back down again. The key to this type of motion is that the velocity at the peak is momentarily, zero. For calculus students, you should already know that the derivative at the maximum or minimum of a quadratic function is always going to be zero, and since our equation $y=v_0t-\frac 1 2 gt^2$, models displacement, the time derivative of displacement is just velocity. So the derivative at the maximum of that function is zero, which means the velocity there is zero.

So, what are the equations that we can derive from this? Let's find the total time that the object is in the air. If you throw it up and it comes back to you, the total vertical displacement is zero. $$0=v_0t-\frac 1 2 gt^2$$ $$0=(v_0-\frac 1 2 gt)t$$ $$t=0,\frac{2v_0}{g}$$ The second option is a much more meaningful answer than the first one, since we obviously know the vertical displacement is zero at $t=0$. Now what about the maximum height the object reaches? The object is traveling upwards, which we define to be the positive direction, so $\Delta y=h$. We will also utilize the fact that the velocity at the top is momentarily zero: $$y=h=v_0t-\frac 1 2 gt^2$$ $$(0)=v_0-gt$$ $$t=\frac{v_0}{g}$$ Notice that the time to reach the top is the same to reach the bottom, which will bring up an important concept. Since it takes half the time to go from $v_0$ to zero, then the other half of the time must be going from $0$ to $-v_0$ (Plug the previously derived equation for $t$ into $v_f=v_0-gt$ to see for yourself).

Thus, the velocity of the object when it returns to its original height after being thrown upwards with velocity $v_0$ is $-v_0$. The same magnitude of velocity, but in opposite directions. Now plugging the time $t$ it takes to reach height $h$: $$h=v_0(\frac{v_0}{g}) - \frac 1 2 g(\frac{v_0}{g})^2=\frac{v_0^2}{2g}$$ We don't have any specific problems for you to solve on this concept, but it becomes more important and more prevalent in the next chapter.

Conclusion

Ok! Have you mastered one-dimensional motion? Are you ready to try your hand at two-dimensional motion? Then hit "Next Lesson" to go to it!

Next Lesson! →